Ohm Solver: Magnetic Reconnection
Hybrid-PIC codes are often used to simulate magnetic reconnection in space plasmas. An example of magnetic reconnection from a force-free sheet is provided, based on the simulation described in Le et al. [14].
Run
The following Python script configures and launches the simulation.
Script inputs_test_2d_ohm_solver_magnetic_reconnection_picmi.py
Listing 51 You can copy this file from
Examples/Tests/ohm_solver_magnetic_reconnection/inputs_test_2d_ohm_solver_magnetic_reconnection_picmi.py.#!/usr/bin/env python3
#
# --- Test script for the kinetic-fluid hybrid model in WarpX wherein ions are
# --- treated as kinetic particles and electrons as an isothermal, inertialess
# --- background fluid. The script demonstrates the use of this model to
# --- simulate magnetic reconnection in a force-free sheet. The setup is based
# --- on the problem described in Le et al. (2016)
# --- https://aip.scitation.org/doi/10.1063/1.4943893.
import argparse
import shutil
import sys
from pathlib import Path
import dill
import numpy as np
from mpi4py import MPI as mpi
from pywarpx import callbacks, libwarpx, picmi
from pywarpx.LoadThirdParty import load_cupy
constants = picmi.constants
comm = mpi.COMM_WORLD
simulation = picmi.Simulation(warpx_serialize_initial_conditions=True, verbose=0)
def get_xp():
xp, _ = load_cupy()
return xp
class ForceFreeSheetReconnection(object):
# B0 is chosen with all other quantities scaled by it
B0 = 0.1 # Initial magnetic field strength (T)
# Physical parameters
m_ion = 400.0 # Ion mass (electron masses)
beta_e = 0.1
Bg = 0.3 # times B0 - guiding field
dB = 0.01 # times B0 - initial perturbation to seed reconnection
T_ratio = 5.0 # T_i / T_e
# Domain parameters
LX = 40 # ion skin depths
LZ = 20 # ion skin depths
LT = 50 # ion cyclotron periods
DT = 1e-3 # ion cyclotron periods
# Resolution parameters
NX = 512
NZ = 512
# Starting number of particles per cell
NPPC = 400
# Plasma resistivity - used to dampen the mode excitation
eta = 6e-3 # normalized resistivity
# Number of substeps used to update B
substeps = 20
def __init__(self, test, verbose):
self.test = test
self.verbose = verbose or self.test
# calculate various plasma parameters based on the simulation input
self.get_plasma_quantities()
self.Lx = self.LX * self.l_i
self.Lz = self.LZ * self.l_i
self.dt = self.DT * self.t_ci
# run very low resolution as a CI test
if self.test:
self.total_steps = 20
self.diag_steps = self.total_steps // 5
self.NX = 128
self.NZ = 128
else:
self.total_steps = int(self.LT / self.DT)
self.diag_steps = self.total_steps // 200
# Initial magnetic field
self.Bg *= self.B0
self.dB *= self.B0
self.Bx = (
f"{self.B0}*tanh(z*{1.0 / self.l_i})"
f"+{-self.dB * self.Lx / (2.0 * self.Lz)}*cos({2.0 * np.pi / self.Lx}*x)"
f"*sin({np.pi / self.Lz}*z)"
)
self.By = (
f"sqrt({self.Bg**2 + self.B0**2}-({self.B0}*tanh(z*{1.0 / self.l_i}))**2)"
)
self.Bz = f"{self.dB}*sin({2.0 * np.pi / self.Lx}*x)*cos({np.pi / self.Lz}*z)"
self.J0 = self.B0 / constants.mu0 / self.l_i
# dump all the current attributes to a dill pickle file
if comm.rank == 0:
with open("sim_parameters.dpkl", "wb") as f:
dill.dump(self, f)
# print out plasma parameters
if comm.rank == 0:
print(
f"Initializing simulation with input parameters:\n"
f"\tTi = {self.Ti * 1e-3:.1f} keV\n"
f"\tn0 = {self.n_plasma:.1e} m^-3\n"
f"\tB0 = {self.B0:.2f} T\n"
f"\tM/m = {self.m_ion:.0f}\n"
)
print(
f"Plasma parameters:\n"
f"\tl_i = {self.l_i:.1e} m\n"
f"\tt_ci = {self.t_ci:.1e} s\n"
f"\tv_ti = {self.vi_th:.1e} m/s\n"
f"\tvA = {self.vA:.1e} m/s\n"
)
print(
f"Numerical parameters:\n"
f"\tdz = {self.Lz / self.NZ:.1e} m\n"
f"\tdt = {self.dt:.1e} s\n"
f"\tdiag steps = {self.diag_steps:d}\n"
f"\ttotal steps = {self.total_steps:d}\n"
)
self.setup_run()
def get_plasma_quantities(self):
"""Calculate various plasma parameters based on the simulation input."""
# Ion mass (kg)
self.M = self.m_ion * constants.m_e
# Cyclotron angular frequency (rad/s) and period (s)
self.w_ce = constants.q_e * abs(self.B0) / constants.m_e
self.w_ci = constants.q_e * abs(self.B0) / self.M
self.t_ci = 2.0 * np.pi / self.w_ci
# Electron plasma frequency: w_pe / omega_ce = 2 is given
self.w_pe = 2.0 * self.w_ce
# calculate plasma density based on electron plasma frequency
self.n_plasma = self.w_pe**2 * constants.m_e * constants.ep0 / constants.q_e**2
# Ion plasma frequency (Hz)
self.w_pi = np.sqrt(constants.q_e**2 * self.n_plasma / (self.M * constants.ep0))
# Ion skin depth (m)
self.l_i = constants.c / self.w_pi
# # Alfven speed (m/s): vA = B / sqrt(mu0 * n * (M + m)) = c * omega_ci / w_pi
self.vA = abs(self.B0) / np.sqrt(
constants.mu0 * self.n_plasma * (constants.m_e + self.M)
)
# calculate Te based on beta
self.Te = (
self.beta_e
* self.B0**2
/ (2.0 * constants.mu0 * self.n_plasma)
/ constants.q_e
)
self.Ti = self.Te * self.T_ratio
# calculate thermal speeds
self.ve_th = np.sqrt(self.Te * constants.q_e / constants.m_e)
self.vi_th = np.sqrt(self.Ti * constants.q_e / self.M)
# Ion Larmor radius (m)
self.rho_i = self.vi_th / self.w_ci
# Reference resistivity (Malakit et al.)
self.eta0 = self.l_i * self.vA / (constants.ep0 * constants.c**2)
def setup_run(self):
"""Setup simulation components."""
#######################################################################
# Set geometry and boundary conditions #
#######################################################################
# Create grid
self.grid = picmi.Cartesian2DGrid(
number_of_cells=[self.NX, self.NZ],
lower_bound=[-self.Lx / 2.0, -self.Lz / 2.0],
upper_bound=[self.Lx / 2.0, self.Lz / 2.0],
lower_boundary_conditions=["periodic", "dirichlet"],
upper_boundary_conditions=["periodic", "dirichlet"],
lower_boundary_conditions_particles=["periodic", "reflecting"],
upper_boundary_conditions_particles=["periodic", "reflecting"],
warpx_max_grid_size=self.NZ,
)
simulation.time_step_size = self.dt
simulation.max_steps = self.total_steps
simulation.current_deposition_algo = "direct"
simulation.particle_shape = 1
simulation.use_filter = False
simulation.verbose = self.verbose
#######################################################################
# Field solver and external field #
#######################################################################
self.solver = picmi.HybridPICSolver(
grid=self.grid,
gamma=1.0,
Te=self.Te,
n0=self.n_plasma,
n_floor=0.1 * self.n_plasma,
plasma_resistivity=self.eta * self.eta0,
substeps=self.substeps,
)
simulation.solver = self.solver
B_ext = picmi.AnalyticInitialField(
Bx_expression=self.Bx, By_expression=self.By, Bz_expression=self.Bz
)
simulation.add_applied_field(B_ext)
#######################################################################
# Particle types setup #
#######################################################################
self.ions = picmi.Species(
name="ions",
charge="q_e",
mass=self.M,
initial_distribution=picmi.UniformDistribution(
density=self.n_plasma,
rms_velocity=[self.vi_th] * 3,
),
)
simulation.add_species(
self.ions,
layout=picmi.PseudoRandomLayout(
grid=self.grid, n_macroparticles_per_cell=self.NPPC
),
)
#######################################################################
# Add diagnostics #
#######################################################################
callbacks.installafterEsolve(self.check_fields)
if self.test:
particle_diag = picmi.ParticleDiagnostic(
name="diag1",
period=self.total_steps,
species=[self.ions],
data_list=["ux", "uy", "uz", "x", "z", "weighting"],
# warpx_format='openpmd',
# warpx_openpmd_backend='h5',
)
simulation.add_diagnostic(particle_diag)
field_diag = picmi.FieldDiagnostic(
name="diag1",
grid=self.grid,
period=self.total_steps,
data_list=["B", "E", "phi"],
# warpx_format='openpmd',
# warpx_openpmd_backend='h5',
)
simulation.add_diagnostic(field_diag)
# set the solver convergence criteria low since phi is only
# calculated for diagnostic output testing
simulation.self_fields_required_precision = 1e-3
simulation.self_fields_verbosity = 1
# reduced diagnostics for reconnection rate calculation
# create a 2 l_i box around the X-point on which to measure
# magnetic flux changes
plane = picmi.ReducedDiagnostic(
diag_type="FieldProbe",
name="plane",
period=self.diag_steps,
path="diags/",
extension="dat",
probe_geometry="Plane",
resolution=60,
x_probe=0.0,
z_probe=0.0,
detector_radius=self.l_i,
target_up_x=0,
target_up_z=1.0,
)
simulation.add_diagnostic(plane)
#######################################################################
# Initialize #
#######################################################################
if comm.rank == 0:
if Path.exists(Path("diags")):
shutil.rmtree("diags")
Path("diags/fields").mkdir(parents=True, exist_ok=True)
# Initialize inputs and WarpX instance
simulation.initialize_inputs()
simulation.initialize_warpx()
def check_fields(self):
step = simulation.extension.warpx.getistep(lev=0) - 1
if not (step == 1 or step % self.diag_steps == 0):
return
get_xp()
rho = simulation.fields.get("rho_fp", level=0)[...] / self.J0
Jiy = simulation.fields.get("current_fp", dir="y", level=0)[...] / self.J0
Jy = (
simulation.fields.get("hybrid_current_fp_plasma", dir="y", level=0)[...]
/ self.J0
)
Bx = simulation.fields.get("Bfield_fp", dir="x", level=0)[...] / self.B0
By = simulation.fields.get("Bfield_fp", dir="y", level=0)[...] / self.B0
Bz = simulation.fields.get("Bfield_fp", dir="z", level=0)[...] / self.B0
if libwarpx.amr.ParallelDescriptor.MyProc() != 0:
return
# save the fields to file
with open(f"diags/fields/fields_{step:06d}.npz", "wb") as f:
np.savez(f, rho=rho, Jiy=Jiy, Jy=Jy, Bx=Bx, By=By, Bz=Bz)
##########################
# parse input parameters
##########################
parser = argparse.ArgumentParser()
parser.add_argument(
"-t",
"--test",
help="toggle whether this script is run as a short CI test",
action="store_true",
)
parser.add_argument(
"-v",
"--verbose",
help="Verbose output",
action="store_true",
)
args, left = parser.parse_known_args()
sys.argv = sys.argv[:1] + left
run = ForceFreeSheetReconnection(test=args.test, verbose=args.verbose)
simulation.step()
Running the full simulation should take about 4 hours if executed on 1 V100 GPU.
For MPI-parallel runs, prefix these lines with
mpiexec -n 4 ... or srun -n 4 ..., depending on the system.
python3 inputs_test_2d_ohm_solver_magnetic_reconnection_picmi.py
Analyze
The following script extracts the reconnection rate as a function of time and animates the evolution of the magnetic field (as shown below).
Script analysis.py
Listing 52 You can copy this file from
Examples/Tests/ohm_solver_magnetic_reconnection/analysis.py.#!/usr/bin/env python3
#
# --- Analysis script for the hybrid-PIC example of magnetic reconnection.
import glob
import dill
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors
plt.rcParams.update({"font.size": 20})
# load simulation parameters
with open("sim_parameters.dpkl", "rb") as f:
sim = dill.load(f)
x_idx = 2
z_idx = 4
Ey_idx = 6
Bx_idx = 8
plane_data = np.loadtxt("diags/plane.dat", skiprows=1)
steps = np.unique(plane_data[:, 0])
num_steps = len(steps)
num_cells = plane_data.shape[0] // num_steps
plane_data = plane_data.reshape((num_steps, num_cells, plane_data.shape[1]))
times = plane_data[:, 0, 1]
dt = np.mean(np.diff(times))
plt.plot(
times / sim.t_ci,
np.mean(plane_data[:, :, Ey_idx], axis=1) / (sim.vA * sim.B0),
"o-",
)
plt.grid()
plt.xlabel(r"$t/\tau_{c,i}$")
plt.ylabel("$<E_y>/v_AB_0$")
plt.title("Reconnection rate")
plt.tight_layout()
plt.savefig("diags/reconnection_rate.png")
if not sim.test:
from matplotlib.animation import FFMpegWriter, FuncAnimation
from scipy import interpolate
# Animate the magnetic reconnection
fig, axes = plt.subplots(3, 1, sharex=True, figsize=(7, 9))
for ax in axes.flatten():
ax.set_aspect("equal")
ax.set_ylabel("$z/l_i$")
axes[2].set_xlabel("$x/l_i$")
datafiles = sorted(glob.glob("diags/fields/*.npz"))
num_steps = len(datafiles)
data0 = np.load(datafiles[0])
sX = axes[0].imshow(
data0["Jy"].T,
origin="lower",
norm=colors.TwoSlopeNorm(vmin=-0.6, vcenter=0.0, vmax=1.6),
extent=[0, sim.LX, -sim.LZ / 2, sim.LZ / 2],
cmap=plt.cm.RdYlBu_r,
)
# axes[0].set_ylim(-5, 5)
cb = plt.colorbar(sX, ax=axes[0], label="$J_y/J_0$")
cb.ax.set_yscale("linear")
cb.ax.set_yticks([-0.5, 0.0, 0.75, 1.5])
sY = axes[1].imshow(
data0["By"].T,
origin="lower",
extent=[0, sim.LX, -sim.LZ / 2, sim.LZ / 2],
cmap=plt.cm.plasma,
)
# axes[1].set_ylim(-5, 5)
cb = plt.colorbar(sY, ax=axes[1], label="$B_y/B_0$")
cb.ax.set_yscale("linear")
sZ = axes[2].imshow(
data0["Bz"].T,
origin="lower",
extent=[0, sim.LX, -sim.LZ / 2, sim.LZ / 2],
# norm=colors.TwoSlopeNorm(vmin=-0.02, vcenter=0., vmax=0.02),
cmap=plt.cm.RdBu,
)
cb = plt.colorbar(sZ, ax=axes[2], label="$B_z/B_0$")
cb.ax.set_yscale("linear")
# plot field lines
x_grid = np.linspace(0, sim.LX, data0["Bx"][:-1].shape[0])
z_grid = np.linspace(-sim.LZ / 2.0, sim.LZ / 2.0, data0["Bx"].shape[1])
n_lines = 10
start_x = np.zeros(n_lines)
start_x[: n_lines // 2] = sim.LX
start_z = np.linspace(-sim.LZ / 2.0 * 0.9, sim.LZ / 2.0 * 0.9, n_lines)
step_size = 1.0 / 100.0
def get_field_lines(Bx, Bz):
field_line_coords = []
Bx_interp = interpolate.interp2d(x_grid, z_grid, Bx[:-1].T)
Bz_interp = interpolate.interp2d(x_grid, z_grid, Bz[:, :-1].T)
for kk, z in enumerate(start_z):
path_x = [start_x[kk]]
path_z = [z]
ii = 0
while ii < 10000:
ii += 1
Bx = Bx_interp(path_x[-1], path_z[-1])[0]
Bz = Bz_interp(path_x[-1], path_z[-1])[0]
# print(path_x[-1], path_z[-1], Bx, Bz)
# normalize and scale
B_mag = np.sqrt(Bx**2 + Bz**2)
if B_mag == 0:
break
dx = Bx / B_mag * step_size
dz = Bz / B_mag * step_size
x_new = path_x[-1] + dx
z_new = path_z[-1] + dz
if (
np.isnan(x_new)
or x_new <= 0
or x_new > sim.LX
or abs(z_new) > sim.LZ / 2
):
break
path_x.append(x_new)
path_z.append(z_new)
field_line_coords.append([path_x, path_z])
return field_line_coords
field_lines = []
for path in get_field_lines(data0["Bx"], data0["Bz"]):
path_x = path[0]
path_z = path[1]
(ln,) = axes[2].plot(path_x, path_z, "--", color="k")
# draws arrows on the field lines
# if path_x[10] > path_x[0]:
axes[2].arrow(
path_x[50],
path_z[50],
path_x[250] - path_x[50],
path_z[250] - path_z[50],
shape="full",
length_includes_head=True,
lw=0,
head_width=1.0,
color="g",
)
field_lines.append(ln)
def animate(i):
data = np.load(datafiles[i])
sX.set_array(data["Jy"].T)
sY.set_array(data["By"].T)
sZ.set_array(data["Bz"].T)
sZ.set_clim(-np.max(abs(data["Bz"])), np.max(abs(data["Bz"])))
for ii, path in enumerate(get_field_lines(data["Bx"], data["Bz"])):
path_x = path[0]
path_z = path[1]
field_lines[ii].set_data(path_x, path_z)
anim = FuncAnimation(fig, animate, frames=num_steps - 1, repeat=True)
writervideo = FFMpegWriter(fps=14)
anim.save("diags/mag_reconnection.mp4", writer=writervideo)
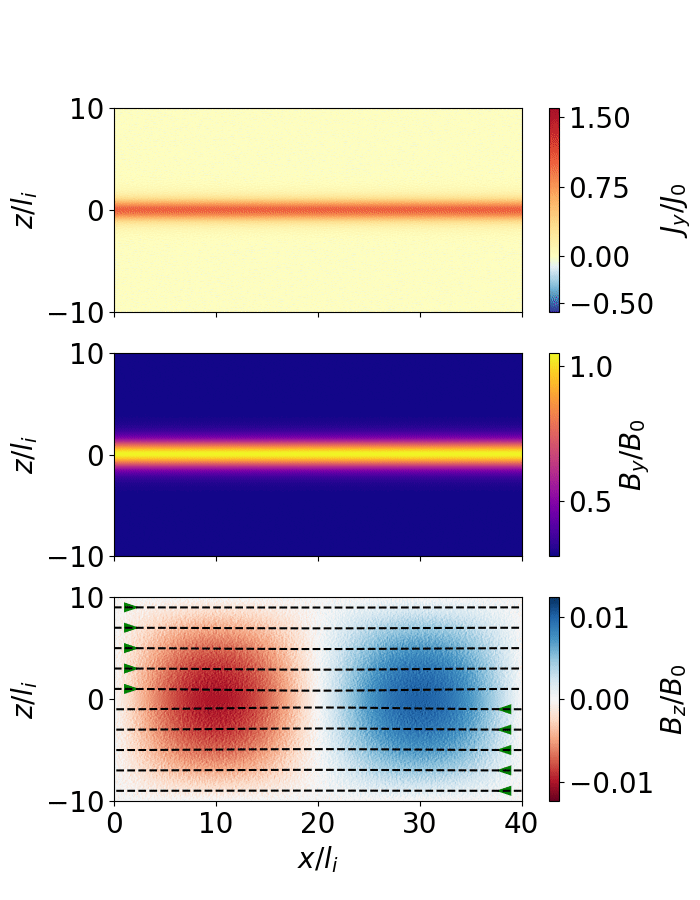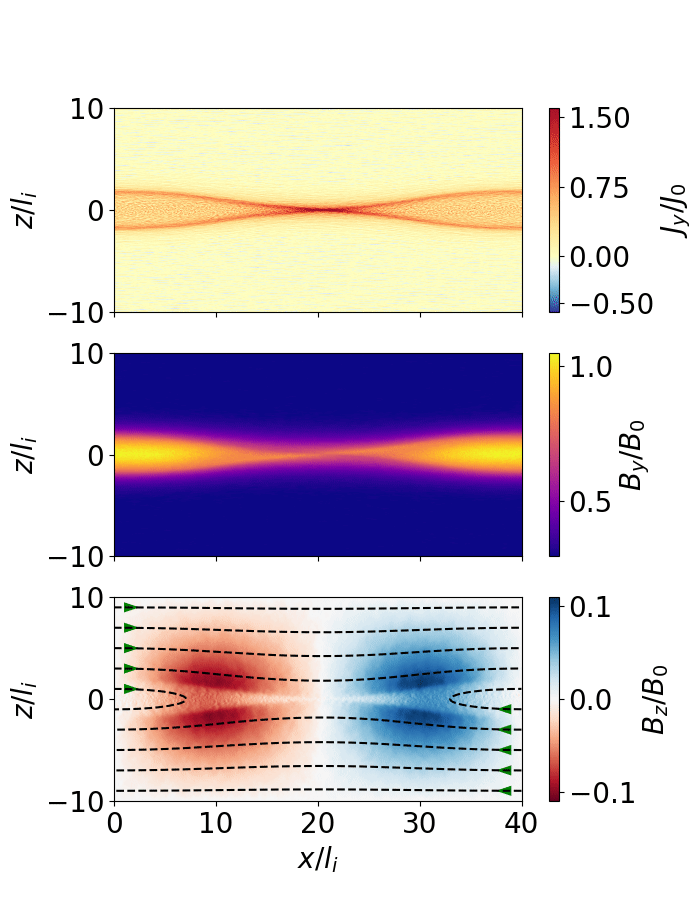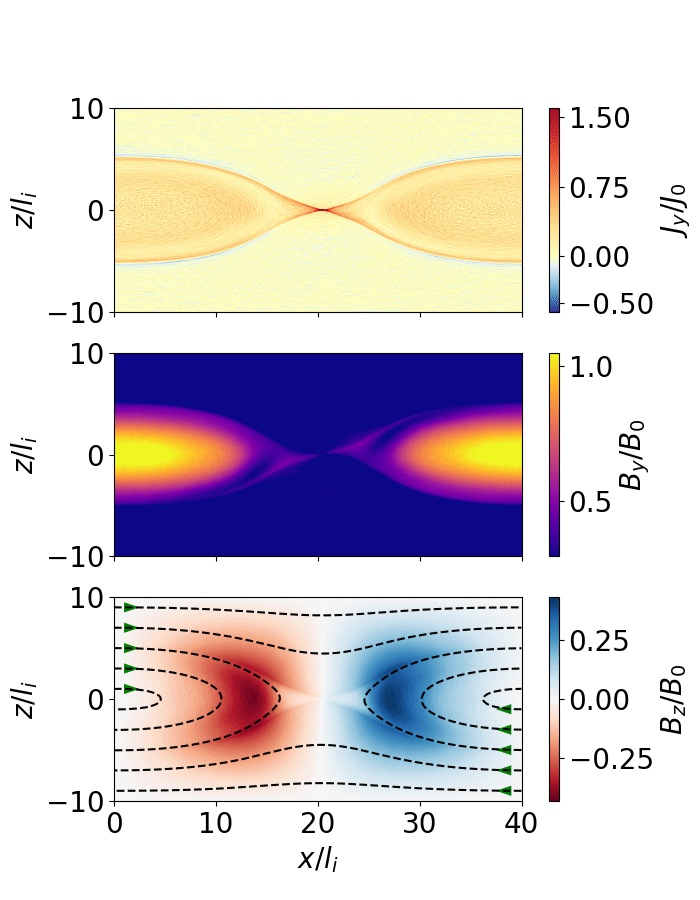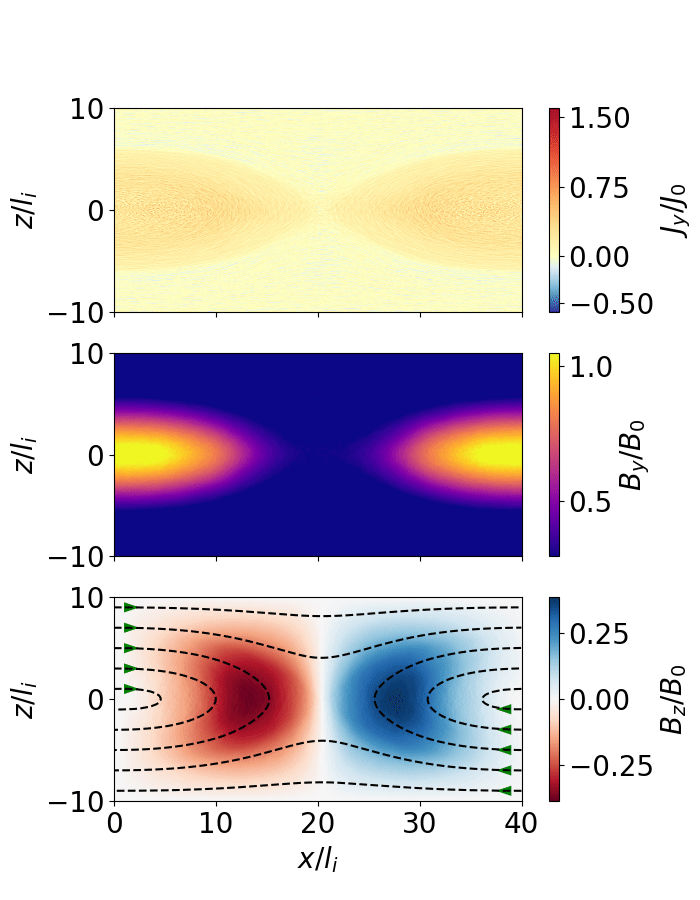
Fig. 10 Magnetic reconnection from a force-free sheet.